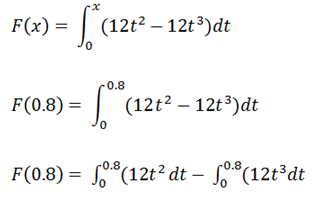CUADRO COMPARATIVO ENTRE LAS DISTRIBUCIONES

Redactor(es):

Karla Santamaria CI 26.596.909

Brian Rodriguez CI 27.820.343

Julianny Campos CI 25.389.158

Ronney Matloo CI 27.262.543

 Distribucion de Probabilidad Hipergeometrica

La distribución hipergeométrica es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realicen experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial.

Es una distribución fundamental en el estudio de muestras pequeñas de poblaciones pequeñas y en el cálculo de probabilidades de juegos de azar. Tiene grandes aplicaciones en el control de calidad para procesos experimentales en los que no es posible retornar a la situación de partida.

Las consideraciones a tener en cuenta en una distribución hipergeométrica:

·       El proceso consta de "n" pruebas, separadas o separables de entre un conjunto de "N" pruebas posibles.

·       Cada una de las pruebas puede dar únicamente dos resultados mutuamente excluyentes.

·       El número de individuos que presentan la característica A (éxito) es "k".

·       En la primera prueba las probabilidades son: P(A)= p y P(A)= q; con p+q=1.

En estas condiciones, se define la variable aleatoria X = “nº de éxitos obtenidos”. La función de probabilidad de esta variable sería:

La media, varianza y desviación típica de esta distribución vienen dadas por:

Un ejemplo del empleo de esta distribución es el siguiente:

“De cada 20 piezas fabricadas por una máquina, hay 2 que son defectuosas. Para realizar un control de calidad, se observan 15 elementos y se rechaza el lote si hay alguna que sea defectuoso.”

Vamos a calcular la probabilidad de que el lote sea rechazado.

Redactor:

Brian Rodriguez

C.I 27820343

Referencias bibliográficas:

Juan Cañas (2022) 4.1. Distribución hipergeométrica. Recuperado de: https://proyectodescartes.org/iCartesiLibri/materiales_didacticos/EstadisticaProbabilidadInferencia/VAdiscreta/4_1DistribucionHipergeometrica/index.html

Distribución de Probabilidad Geométrica

La Distribución Geométrica consiste en una serie de ensayos donde pueden ocurrir éxitos o fracasos, cada ensayo es idéntico e independiente del otro, pero no hay un número fijo de ensayos, sino que el experimento se repite hasta que se consiga el éxito. Es una distribución de tipo discreta, que puede modelar el número de ensayos consecutivos necesarios para observar el resultado de interés por primera vez. La distribución geométrica también puede modelar el número de no eventos que ocurren antes de que se observe el primer resultado.

Por ejemplo, una distribución geométrica puede modelar probabilidades como el lanzamiento de una moneda o puede modelar en una línea de ensamble, el número de unidades producidas antes de que se produzca la primera unidad defectuosa.

Esta distribución se puede aplicar de dos formas utilizando las siguientes formulas según sea el caso:

1.     ¿Cuántos fallos necesito antes de obtener el éxito?

Hablar del caso X=2 o cuando X=3, es lo mismo que decir que yo quiero obtener el éxito en el ensayo número 2 o 3, por lo tanto, se debió de haber fracasado en los ensayos anteriores. Si yo quiero el éxito en el ensayo 2, se tuvo que haber fracasado en el primer ensayo, esto es lo que explica a la ecuación, lo mismo pasa cuando X=3, si yo quiero el éxito sólo en el ensayo 3, se tuvo que haber fracasado en el primer ensayo y en el segundo ensayo.

2.     ¿Y si quiero éxito en todos mis ensayos?

Retomando el mismo ejemplo de la línea de producción, si sabemos que la línea de producción tiene una probabilidad del 60% de éxito por cada objeto, y se desea saber cual es la probabilidad de que se produzcan al menos 3 objetos con éxito, se aplicaría la formula de la siguiente forma:

De manera que, la probabilidad de que se produzcan 3 objetos seguidos con éxito y sin defectos es del 21.6%

Propiedades de la distribución de probabilidad Geométrica:

Esperanza:

Varianza:

Distribución Acumulada:

Redactor:

Brian Rodriguez

C.I 27820343

Referencias bibliográficas:

(2021) Explicación y ejemplos de la distribución geométrica. Recuperado de: https://www.rbjlabs.com/probabilidad-y-estadistica/explicacion-ejemplos-distribucion-geometrica/

Juan Cañas (2022) 4.3. Distribución Geométrica. Recuperado de: https://proyectodescartes.org/iCartesiLibri/materiales_didacticos/EstadisticaProbabilidadInferencia/VAdiscreta/4_3DistribucionGeometrica/index.html

 

Distribución De Probabilidad Gamma. 

     la distribución gamma se utiliza para modelar valores de datos positivos que sean asimétricos a la derecha y mayores que 0. La distribución gamma se utiliza comúnmente en estudios de supervivencia de fiabilidad. Por ejemplo, la distribución gamma puede describir el tiempo que transcurre para que falle un componente eléctrico. La mayoría de los componentes eléctricos de un tipo particular fallará aproximadamente en el mismo momento, pero unos pocos tardarán más en fallar.

Función Gamma.

para α > 0

Función de densidad. 

Para x > 0, α > 0 y β > 0

Propiedades de la distribución Gamma:

Media: 

Varianza:

Función de distribución Gamma.

Ejercicio práctico

     en cierta ciudad el consumo diario de energía eléctrica, en millones de kilowatts-hora, es una variable aleatoria x que tiene una distribución gamma con media µ= 6 y varianza = 12

• A)   Calcule los valores de α y β
• B)   Calcule la probabilidad de que en cualquier día dado el consumo de energía eléctrico exceda los 12 millones de kilowatts-hora.

Solución:

a)

 

 

 

la probabilidad de que en cualquier día dado el consumo de energía eléctrico exceda los 12 millones de kilowatts-hora es 0,0619

Redactor:

Julianny Campos

C.I 25389158

Referencias bibliográficas:

https://support.minitab.com/es-mx/minitab/18/help-and-how-to/probability-distributions-and-random-data/supporting-topics/distributions/gamma-distribution/

https://www.youtube.com/watch?v=fLeSndsVwWw&list=PLMQiXZ0fz12niOVghveJdjhwICoswvrcp&index=125

 

Distribución de probabilidad βeta.

     La distribución beta es una familia de distribuciones continuas de probabilidad definidas en el intervalo [0,1] parametrizada por dos parámetros positivos de forma, denotados por α y β, que aparecen como exponentes de la variable aleatoria y controlan la forma de la distribución.

La generalización de esta distribución a varias variables es conocida como la distribución de Dirichlet.

Ambas formas son iguales a 1

Cuando ambas formas son iguales a 1, la distribución beta es la distribución uniforme.

Ambas formas son menores que 1

Cuando ambas formas son menores que 1, la distribución tiene forma de U.

 

Ambas formas son iguales y son mayores que 1

Cuando ambas formas son iguales y mayores que 1, la distribución es simétrica.

La primera forma es mayor que la segunda forma

Cuando la primera forma es mayor que la segunda forma, la distribución es asimétrica hacia la izquierda..

La primera forma es menor que la segunda forma

Cuando la primera forma es menor que la segunda forma, la distribución es asimétrica hacia la derecha.

Función βeta

Función de densidad.

Para 0 < x < 1

Función de distribución βeta

Para 0 < X < 1

Propiedades de la distribución βeta

Media:

Varianza:

función de distribución de βeta

Ejercicio práctico

Si la proporción de una marca de computadoras que requieren servicios técnicos durante el primer año de operación es una variable aleatoria que tiene una distribución beta con α = 3 y β = 2, ¿Cuál es la probabilidad de que  al menos 80% de los nuevos modelos de esta marca que se vieron este año requieren servicio técnico durante su primer año de operación? 

función de densidad

sustituimos los valores

se utilizara la variable t en el lugar de la variable x para no repetirla, ya que se encuentra en los limites de integración.

la función de distribución acumulada viene dada por:

 

la probabilidad de que al menos el 80%  de los nuevos modelos que se vendieron este año requieren servicio técnico durante su primer año de operación es de:   

Redactor:

Julianny Campos 

C.I 25389158

referencias bibliográficas:

https://www.youtube.com/watch?v=atx_UTKb7hU&t=22s

https://es.wikipedia.org/wiki/Distribuci%C3%B3n_beta#Funci%C3%B3n_de_densidad

support.minitab.com/es-mx/minitab/18/help-and-how-to/probability-distributions-and-random-data/supporting-topics/distributions/beta-distribution/

 

 

 

DISTRIBUCIÓN DE PROBABILIDAD DE POISSON

Proporciona la probabilidad de que ocurra un determinado suceso un número de veces K en un intervalo. Dicho, intervalo puede ser de tiempo, longitud, área, entre otros.

Formulas:

Ejercicio Practico

El ingeniero Franklin Acosta desarrolla en promedio actualizaciones para aplicaciones 3 veces a la semana. Calcular la probabilidad de: 1) Que desarrolle 2 o más actualizaciones para aplicaciones, pero menos de 5, en una semana. 2) Calcule la media, la varianza y la desviación estándar.

Antes de comenzar, extraemos los datos del ejercicio:

Respuesta 1)

En este caso, nos están preguntando la probabilidad de que la variable aleatoria X sea menor que 5 y tiene que ser mayor o igual a 2. Por lo tanto, la solución sería de la siguiente manera:

Respuesta 2)

Aplicando las fórmulas correspondientes y sustituyendo valores tenemos que:

Y, culminamos con el ejercicio.

Link del Video subido a YouTube: 

https://youtu.be/X5JOes64l1w

Redactor:

Karla Santamaria 

CI 26.596.909

Referencias Bibliográficas:

DeGroot M. (1988). Probabilidad y estadística. Segunda Edición. Universidad de Valencia.

DISTRIBUCIÓN DE PROBABILIDAD BINOMIAL

Este tipo de distribución resulta de contar el número de éxitos al repetir un experimento n-veces con la particularidad de que ese experimento solamente tiene dos posibles resultados: el éxito (denominado p), y el fracaso (denominado q).

Formulas:

Ejemplo Practico

En una fábrica de equipos de computación se encuentran 20 equipos en los almacenes. El encargado de la fábrica contrata a un ingeniero para saber la calidad de los equipos. La probabilidad de que algún equipo no sea defectuoso es de 0.3. Calcular: 1) La probabilidad de que, al chequear la calidad de los equipos, se encuentren menos de 3 en buen estado. 2) Calcular la media, la varianza y la desviación Estándar.

Primero que nada se extraen los datos necesarios para la realización del ejercicio:

Respuesta 1)

Sería la probabilidad de que la variable aleatoria tome un valor más pequeño que 3, lo que sería igual a la probabilidad de que se tome el valor 0, más el valor 1, más el valor 2. Es decir, la probabilidad de que ningún equipo este en buen estado, de que un equipo este en buen estado, y de que 2 equipos estén en buen estado. Por lo tanto:

Una vez teniendo esto claro, se procede a aplicar la Función de Probabilidad, para cada uno de estos casos, y así, sustituyendo valores y operando, se tiene que:

Respuesta 2)

Aplicando las fórmulas correspondientes y sustituyendo valores, tenemos que:

Y, así se culmina el ejercicio.

Redactor:

Karla Santamaria 

CI 26.596.909

Referencias Bibliográficas:

DeGroot M. (1988). Probabilidad y estadística. Segunda Edición. Universidad de Valencia.

DISTRIBUCIÓN DE PROBABILIDAD EXPONENCIAL

 

DISTRIBUCIÓN DE PROBABILIDAD EXPONENCIAL

La distribución Exponencial es una forma de distribución Poisson en la cual se utiliza su metodología si se quiere calcular los eventos que transcurren en un lapso de tiempo que ocurren cuando estos suceden de manera consecutiva de tipo Poisson este se le conoce como una variable de distribución exponencial.

Esta considera que una variable continua X define el tiempo en el que ocurre dos eventos consecutivos y se establece de la siguiente forma:

Dada una variable aleatoria X que tome valores reales no negativos {x ³ 0} diremos que tiene una distribución exponencial de parámetro a con a ³ 0, si y sólo si su función de densidad tiene la expresión: 

Donde la función de densidad exponencial para la variable exponencial es:

Donde

Λ > 0

e = 2,718281

X  ≥ 0 

Para que esto se pueda cumplir F(x) deben cumplirse las condiciones 

La Esperanza:

La Varianza es:

Ejemplo Practico:

Podemos modelar el tiempo que transcurre hasta que un cliente arribe al sector de cajas como una variable con distribución exponencial de parámetro Λ = 6 clientes por minuto.

Entonces

X ~ Exp (Λ = 6)

a)    a)  El tiempo promedio en que llegan los clientes a caja

a)  b)   La probabilidad de que transcurra a lo sumo medio minuto hasta que llegue un cliente a las cajas

a)      c) La probabilidad de que transcurra por lo menos 1 minuto hasta que llegue un cliente a las cajas

a)     d)  La probabilidad de que el próximo cliente demore entre 10 y 20 segundos en arribar a las cajas 

Redactor::

Ronney Matloo 

V-27.262.543

Bibliografía:

https://www.uv.es/ceaces/base/modelos%20de%20probabilidad/exponencial.htm

https://www.youtube.com/watch?v=ajY_el0_tCE

https://virtual.uptc.edu.co/ova/estadistica/docs/libros/ftp.bioestadistica.uma.es/libro/node78.htm